前言
钛合金点阵作为一种在空间上由单胞周期性排列的轻质结构材料,具有高比强度、高比刚度、良好的吸能特性以及热隔离和声学隔离性能等,广泛应用于航空航天、汽车、生物医学等领域 [1]。然而,由于其高度复杂的空间结构特征,点阵结构难以通过传统制造工艺进行制备。随着增材制造技术,特别是选区激光熔化 (Selective laser melting, SLM) 技术的成熟,为制备复杂精细的点阵结构提供了新的途径 [2-3]。体心四方 (Body-centered tetragonal, BCT)、体心立方 (Body-centered cubic, BCC)、面心立方 (Face-centered cubic, FCC) 以及衍生的点阵结构已在相关文献中得到了广泛研究 [4-6]。相比于其他点阵结构,BCT 点阵结构在 3D 打印中更易形成连续的点阵结构,从而显著提升其压缩强度和韧性。此外,BCT 点阵结构还拥有更大的设计自由度,使其逐渐成为业界最具发展潜力的轻质结构材料之一 [7-8]。
然而,BCT 点阵结构在实际压缩过程中会引发节点连接处的应力集聚现象,从而导致整体结构的压缩失效。熊飞 [9] 通过对 BCT 点阵结构进行单向压缩发现,在受压时 BCT 点阵结构节点处会产生应力集中,其应力远高于连杆部分。为了改进节点区域结构,提高点阵结构整体力学性能和吸能潜力,WU 等 [10-11] 基于 BCC 点阵结构进行节点加强设计,发现加强后结构相较于 BCC 可显著降低应力集中并提升结构的整体抗压性能。姚定烨等 [12] 通过提高激光功率制备出的节点增强型 BCT 点阵结构较之常规 BCT 结构,比抗压强度增加了 52%,显著提升了点阵结构整体的抗压能力。
但受限于实验成本,现有的研究尚未充分探究不同尺寸的加强结构对 BCT 点阵结构性能的影响。有限元仿真作为一种近似的计算方法,因其稳定性和收敛性好,能以较小的代价实现设计迭代,为点阵结构节点加强研究提供了新的思路。孙思远等 [13] 将有限仿真预测的体心立方结构压缩响应与实验数据保持高度一致,证明了有限元分析方法在改进点阵结构方面的可行性。ZHAO 等 [14-15] 通过有限元法优化了常规点阵结构的节点加强形式,显著改善了典型点阵结构的应力分布。
有限元仿真的主要目标之一是表征材料性能以设计工程结构。当前有限元仿真中,点阵结构的力学本构参数一般采用对应的母材力学本构参数开展研究。然而,SLM 工艺在制备点阵结构材料时存在尺寸效应 [16-17]。组成单胞的微支柱存在不可避免的内部微孔洞、表面孔隙缺陷和表面颗粒附着,使得点阵结构微支柱力学性能相较母材块体结构力学性能存在较大差异 [18]。CAO 等 [19] 通过对使用母材本构参数的理想有限元模型进行仿真并与实验室制备点阵结构的压缩性能对比,发现因为微支柱的几何缺陷导致理想模型的预测结果与实验结果存在较大差异,其中抗压强度误差为 18.57%,平台应力误差为 364.15%。LI 等 [20] 发现增材制造工艺得到的 TC4 钛合金点阵结构力学性能受微支柱的内部微孔洞、表面孔隙缺陷和颗粒附着影响显著,并且增加了节点附近发生局部断裂的风险。HOSSAIN 等 [21] 发现 SLM 工艺制备出的点阵单胞微支柱受拉时的屈服强度会下降 29% 到 57%。ARAGHI 等 [22] 通过增材制造工艺制备了与 BCC 点阵结构微支柱直径一致的拉伸试样,经拉伸测试发现材料力学性能相较于母材力学性能下降显著,其中弹性模量下降 5%,屈服强度下降 30%,最大应力下降 24%,并且通过提取微支柱力学本构参数进行点阵结构仿真与实验结果拟合情况较好。因此在对点阵结构开展有限元仿真分析时,应先对制备工艺引起的微支柱本构参数变化情况进行参数识别。
为此,在本研究中,首先建立 Ti-6Al-4V 钛合金 BCT 点阵结构准静态压缩有限元模型,通过试错法识别钛合金点阵结构力学本构参数,使仿真得到的点阵结构应力应变曲线与实验曲线相吻合,从而确定 SLM 制备的钛合金点阵结构微支柱的力学本构参数。并进一步借助有限元仿真分析 BCT 常规点阵结构内部的变形失效过程。在此基础上,通过对承压性能较为薄弱的节点连接区域进行结构加强优化,探究节点加强区域长度和直径变化对 BCT 点阵结构整体压缩性能的影响规律,为航空航天轻量化承压部件的内部点阵结构优化提供技术支撑。
1、方法与原理
1.1 BCT 点阵结构相对密度
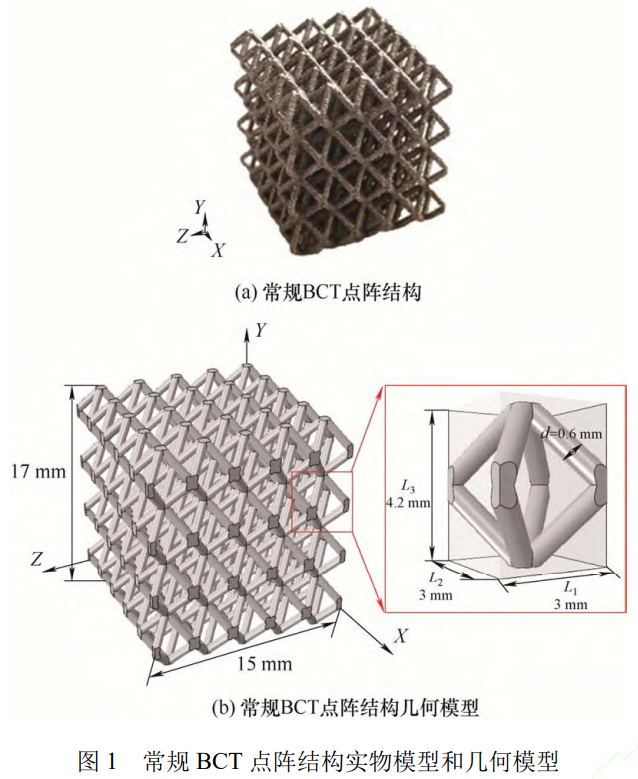
点阵结构的相对密度反映了离散芯体和同厚度实心芯体的比例关系。作为描述点阵材料轻质化程度的普遍指标,相对密度是影响点阵结构力学性能的关键参数之一。由于点阵结构由周期性排列的胞元构成,本文将以胞元的相对密度代替整体结构的相对密度。由图 1b 中胞元几何模型可得,胞元中截面为圆形的每根单杆的体积Vl为:

式中,Vl,V2,V3分别为 BCT 胞元结构的实心长方体芯体的长、宽、高;d 为单杆半径。
胞元的同厚度实心芯体所占空间体积VB为:

根据相对密度的定义可进一步计算 BCT 点阵结构的相对密度ρ-。
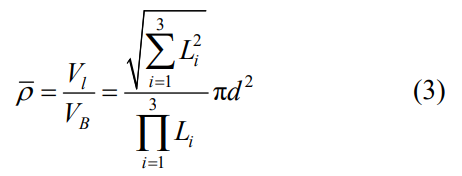
1.2 BCT 点阵结构能量吸收
点阵结构的能量吸收是指结构在受冲击、振动、压缩等加载时,通过结构变形和破坏过程来转换外部机械能量为内部化学能的能力。点阵结构单位体积的能量吸收 (Energy absorption, EA) 可以从工程应力应变曲线和相应的给定应变所围成的积分面积得到,其公式为:
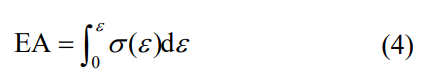
式中,ε表示工程应变,σ(ε) 表示相应的工程应力。
在本文中,随着点阵结构几何模型发生变化,点阵结构的相对密度也随之改变。为了排除相对密度变化对于点阵结构能量吸收性能的影响,需要引入比能量吸收 (Specific energy absorption, SEA)。比能量吸收是指点阵结构在单位质量条件下吸收的能量,与实心材料相比,反映了点阵结构在轻量化设计中的能量转换效率,其公式为:
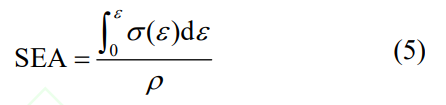
式中,ρ为点阵结构的密度。
此外,点阵结构的承载能力是通过比极限强度来评估的,比极限强度指的是不同应变下相应的抗压强度与点阵结构密度之比,用符号σ-S表示,其公式为:

式中,σs(ε) 为点阵结构的抗压强度。
1.3 钛合金弹塑性力学本构模型
采用各向同性的弹塑性本构模型描述钛合金力学性能。其中弹性变形段为线性,该阶段应力表示为:

式中,σe为弹性段应力,E 为弹性模量,εe为塑性应变。
弹性变形在应力达到屈服点后结束,随后进入塑性硬化阶段,本文中采用指数参数定义塑性硬化阶段,该阶段应力表示为:
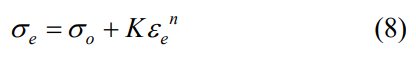
式中,σe为等效应力,σo为屈服强度,K 为强度系数,n 为硬化指数,εe为等效塑性应变。
2、常规 BCT 点阵结构压缩性能仿真
2.1 准静态压缩有限元模拟
本文中,Ti-6Al-4V 钛合金常规 BCT 点阵结构准静态压缩有限元模型分为三个部分:移动的上压盘、固定的下压盘和中间的点阵结构。BCT 点阵结构的三维几何模型如图 1 所示 [12],整体结构由 5×5×4 个胞元组成。胞元的几何参数与姚定烨等 [12] 基于 SLM 工艺制备的点阵实物模型保持一致,胞元密度为0.664g/cm3,其微支柱的直径为 0.6 mm,长度为 3 mm。
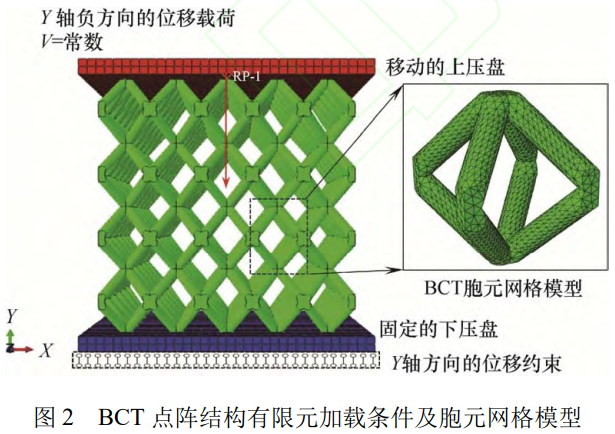
为模拟点阵结构在压缩时的变形演化过程,使用 ABAQUS 的显式动力学求解器进行准静态压缩仿真。保持应变率为0.001s−1,上压盘采用位移边界条件均匀下压 3.39 mm,应变量为模型的 20%。模型的数据采集点位于上压盘中心处,横纵坐标数据集分别为下压方向位移和下压方向支座反力,以此获取模型整体应力应变曲线。准静态压缩加载情况如图 2 所示。
钛合金点阵结构的力学性能采用弹塑性本构模型描述,并使用金属延性损伤表征其损伤失效行为。为获取钛合金母材的弹塑性力学本构参数,参照标准圆柱样品拉伸测试获得的应力应变曲线,从中获取弹性模量、屈服强度及塑性硬化段应力应变数据 [9]。并对一系列塑性硬化段应力应变数据进行拟合得到硬化指数 n 及强度系数 K。详细材料参数如表 1 所示 [9]。
表 1 钛合金 (Ti-6Al-4V) 材料力学本构参数表
| 密度ρ/(kg·m⁻³) | 弹性模量 E/GPa | 泊松比 v | 屈服强度σ0/MPa | 强度系数 K/MPa | 硬化指数 n |
| 4.43 | 118 | 0.3 | 944 | 607.09 | 0.48 |
2.2 有限元模型网格无关性验证
在进行网格划分时,将上压盘作为刚体离散化,点阵结构采用自由网格划分技术进行四面体网格划分。考虑到精度要求和计算效率,需进行网格无关性验证。本文通过控制全局近似单元尺寸设计了 4 组不同网格单元数量的模型,具体数据如表 2 所示。求解后提取应力应变曲线进行对比。因为本文重点关注节点处断裂前的力学性能,故仅对曲线的弹性阶段以及塑性硬化阶段进行分析。
表 2 网格无关性验证模型
| 模型名称 | 单元近似尺寸 /mm | 网格单元数量 / 个 | 计算时间 /h |
| BCT-mesh size-12 | 0.12 | 2 315 550 | 65 |
| BCT-mesh size-17 | 0.17 | 1 386 763 | 33 |
| BCT-mesh size-22 | 0.22 | 790 644 | 24 |
| BCT-mesh size-27 | 0.27 | 625 080 | 19 |
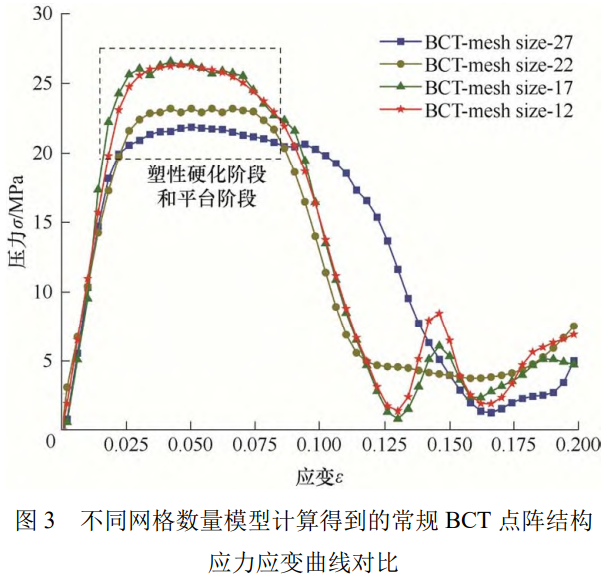
通过对比图 3 不同网格数量模型计算得到的应力应变曲线结果表明,在弹性阶段,随着单元尺寸逐渐减小,曲线的弹性模量呈缓慢上升趋势,当单元尺寸下降到 0.17 mm 时达到临界值。在塑性阶段,当单元尺寸从 0.12 mm 增至 0.17 mm 时,曲线走势及平台段应力值基本不变,而继续增大单元尺寸时曲线发生较大改变,平台段应力值下降显著。因此确定 0.17 mm 为点阵结构网格模型的全局近似单元尺寸,设置单元类型为 C3D10M。胞元网格模型如图 2 所示。
2.3 BCT 点阵结构微支柱材料力学本构参数识别
因实验采用 SLM 工艺制备点阵结构,受工艺限制,微支柱存在内部微孔洞、表面孔隙缺陷和表面颗粒附着,使得点阵结构微支柱力学性能相较母材块体结构力学性能存在较大差异。这种差异不仅影响了点阵结构的整体力学性能,还可能改变损伤方式,从而导致断裂带形貌的变化。为获得能准确描述 SLM 工艺所制备的点阵结构微支柱力学性能的弹塑性本构参数,并使其适用于模拟准静态压缩实验工况的仿真分析,采用试错法 [22],以钛合金母材力学本构参数为初始参数,点阵结构压缩试验获取的应力应变曲线为拟合目标,在一定的取值范围内对弹性模量 E、屈服强度σ0、强度系数 K、硬化指数 n 进行参数识别。通过不断调整仿真输入参数最终使模拟曲线与试验曲线吻合,并输出点阵结构微支柱真实的力学本构参数,进而验证有限元模型的有效性。表 3 为参照相关研究所确定的点阵结构微支柱力学本构参数取值范围 [23-24]。
表 3 点阵结构微支柱力学本构参数识别范围及结果表
| 参数类型 | 弹性模量 E/GPa | 屈服强度σ0/MPa | 强度系数 K/MPa | 硬化指数 n |
| 取值范围 | 102~107 | 750~950 | 200~700 | 0.2~0.6 |
| 结果识别 | 104 | 811 | 214 | 0.45 |
在微支柱力学本构参数取值范围内,对点阵结构开展准静态压缩仿真分析,将得到的应力应变曲线结果与实验结果进行对比,根据两者之间的曲线差异进一步在该范围内调整参数值,直至曲线关键点误差在合理范围内结束有限元仿真,并输出点阵结构微支柱真实的力学本构参数。由于 BCT 点阵结构的独特结构特性,在压缩过程中存在二次坍塌现象,这种非线性行为在有限元模拟中难以精确捕捉。特别是在结构整体首次坍塌后,非均匀塑性流变区的出现使得仿真结果的可靠性降低。并且本文研究目的是分析点阵结构失效前的力学性能和变形情况,因此,在对比应力应变曲线时仅对初期塑性流变区进行分析。
图 4 为微支柱力学本构参数识别前后常规 BCT 点阵结构仿真的应力应变曲线与实验结果的对比。在初期塑性流变区中,各组模型的应力应变曲线均存在线弹性阶段、塑性硬化阶段和应力下降阶段。在弹性阶段时,基于母材力学本构参数的点阵结构仿真模型的等效弹性模量最大,为 0.856 GPa,相较于实验结果高了 93.38%;在微支柱力学本构参数识别后,点阵结构仿真模型的等效弹性模量趋近于实验曲线,为 0.52 GPa,仅比实验结果高了 17.97%。在塑性硬化阶段,基于母材力学本构参数的点阵结构仿真模型在应变值为 0.056 时应力达到峰值,比实验结果提前了 37.5%,且抗压强度比实验结果高了 19.2%。相比之下,在微支柱力学本构参数识别后,点阵结构仿真模型在应变值 0.072 时应力达到峰值,相较于实验结果仅提前了 14.28%,抗压强度相较于实验仅上升 1.46%。因此,经过试错法参数识别,当微支柱力学性能参数中弹性模量为 104 GPa,屈服强度为 811 MPa,强度系数为 214 MPa,硬化指数为 0.45 时,仿真结果和实验结果的拟合情况较好。
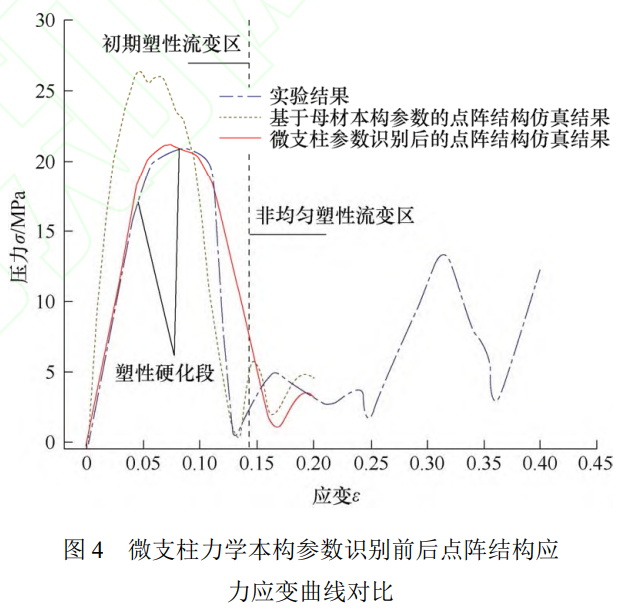
图 5 展示了使用微支柱真实力学本构参数进行的点阵结构仿真的整体失效形式与压缩实验结果的对比情况 [12]。可以看出,仿真模型在坍塌方向上与实验变形一致,均在与压缩载荷方向呈 60° 处出现贯穿整体的坍塌带,且最初的裂纹出现在外围点阵胞元的节点连接处。通过对比典型时刻的应力值发现,此时有限元模拟误差在较小的范围内,变形过程中各阶段的模拟与压缩实验相吻合,与压缩实验的差异主要受制备工艺的限制。由此证明,该模型可在一定程度上模拟准静态压缩实验,模拟结果的可信度较高。

2.4 BCT 常规点阵结构压缩破坏过程分析
图 6 详细展示了常规 BCT 点阵结构在受压时坍塌带的形成过程。由图 6a 可知,当应变量为模型整体的 2.8% 时,点阵结构节点处应力均匀分布,点阵结构各胞元均匀变形。当应变量为模型整体的 9.3% 时,由图 6b 可知,胞元节点处形成了较为明显的应力集中区域。集中区域出现在坍塌带外围上、下端胞元处,应力集中区域最大等效应力值为 1 396 MPa,两者的应力集中区域所分布的位置基本相同。如图 6c 所示,当应变量为模型整体的 12% 时,原先的应力集中区域因为应力值超出了该所能承受的极限,发生了断裂,对于坍塌带外围上端胞元来说,因为横向胞元间节点连接区域发生了断裂,胞元上部杆件失去支撑,在压缩作用下开始向结构内侧倾斜,应力也向倾斜方向传递,带动该方向的下一层胞元节点连接处发生断裂,形成贯穿整体的斜向坍塌带。
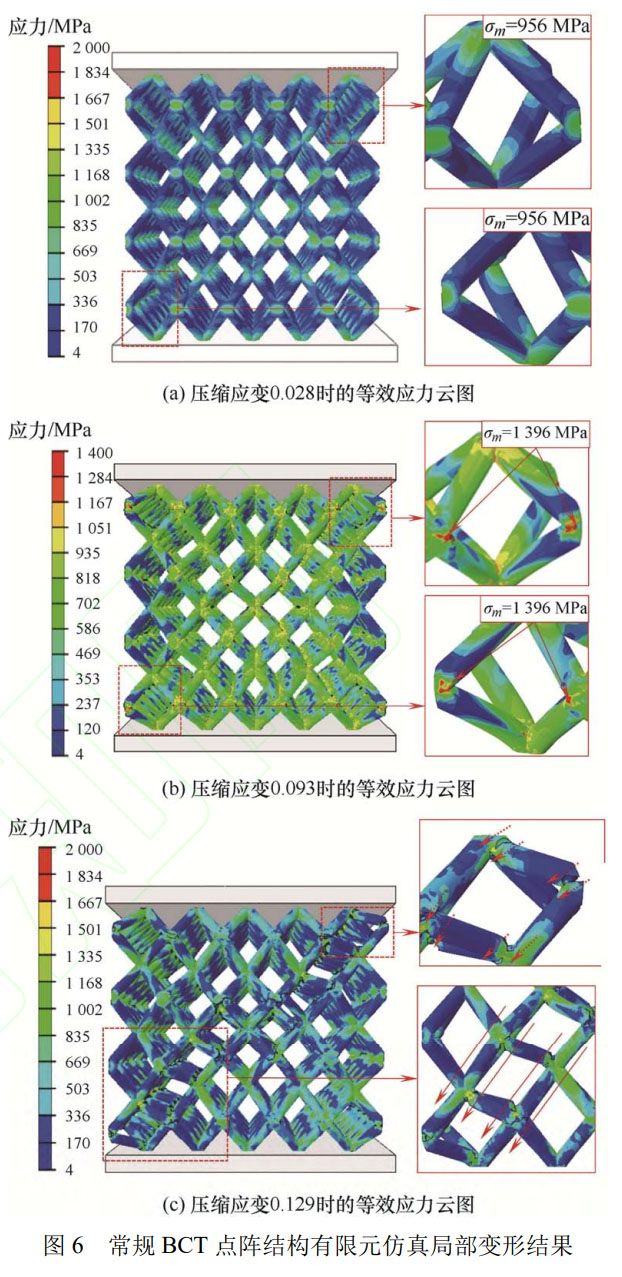
通过对坍塌带上的最外层胞元进行局部分析,发现胞元内部的节点连接区域以及横向胞元间节点连接区域的应力集中现象要大于纵向胞元间节点连接区域,这种现象可能的原因在于胞元间的连接区域所连接的杆件数量为 8 个,大于外侧胞元内部节点所连接的杆件数量,且因为 BCT 胞元的结构特殊性,纵向胞元间连接处的各个杆件夹角小于横向胞元间节点连接区域,从而使胞元间节点的支撑性较好,能够将更多的受力传递到相连的杆件上,降低节点连接处的应力值,使该区域更加稳定。
3、点加强型点阵结构优化分析
3.1 点阵结构胞元数量对其整体压缩性能影响
对于常规 BCT 型点阵结构来说,应力主要集中在连接胞元的横向节点处,且坍塌带也从该区域开始形成,从而导致整体结构失效。所以通过对该区域进行物理结构加强,强化横向节点处的承载能力是提高点阵结构力学性能的重要手段。
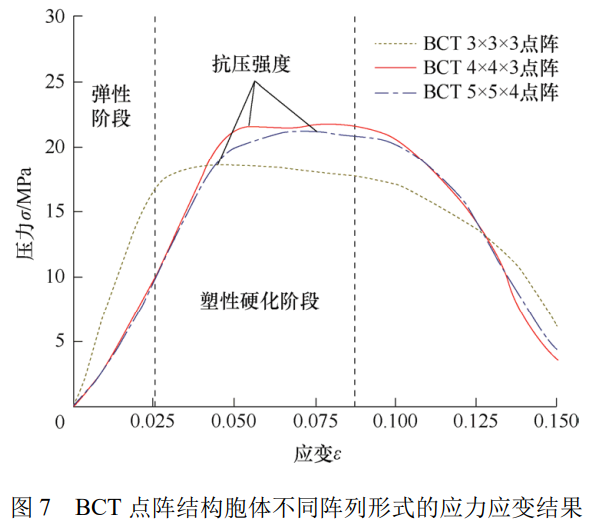
因原结构的 5×5×4 胞元 BCT 点阵结构较为复杂,仿真时间成本较高,不利于后续的节点参数化分析,故针对点阵结构胞元周期性的结构特点进行胞体数量简化。以不影响整体变形趋势和应力分布为目标对 3 组不同胞体数量的点阵结构进行结果对比,以用于后续的局部区域参数化设计。对比图 7 应力应变曲线表明,相较于 3×3×3 个胞元,4×4×3 个胞元的 BCT 点阵结构在弹性段和塑性硬化阶段与原模型基本相似,可以用于后续节点加强仿真分析的替代模型。
3.2 节点加强型点阵结构构型优化仿真
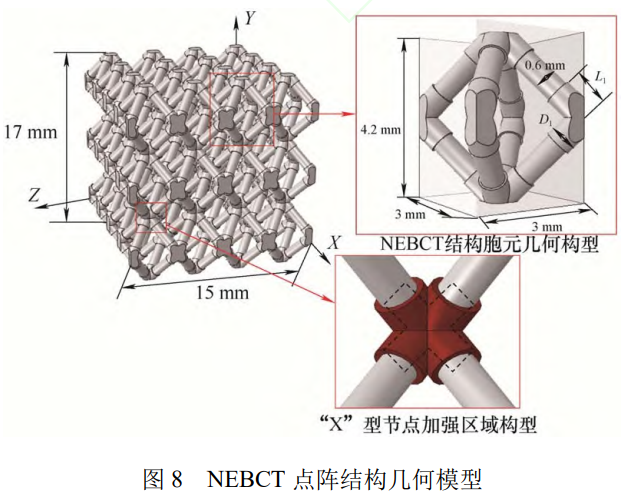
实验通过在节点区域提高激光功率,扩大熔池来熔化更多的粉末颗粒,以增大节点直径的方式进行节点加强 [12]。因为只单独进行了熔化颗粒的增加,未对节点加强区域进行构型控制,这种缺失导致了加强区域形态不规则并伴随着内部孔隙的显著增加,较难实现基于 CT 扫描的真实模型构建,严重影响了后续的仿真分析和结构优化过程。为此,本文在进行模型构建时,基于姚定烨等 [12] 制备点阵模型的节点区域形貌特征,采取了等效均质化的处理方法,设计了一种如图 8 所示的呈 X 构型的节点加强区域,并将模型表面简化为均质光滑表面,得到节点加强型体心四方 (Node enhanced body-centered tetragonal, NEBCT) 点阵结构。
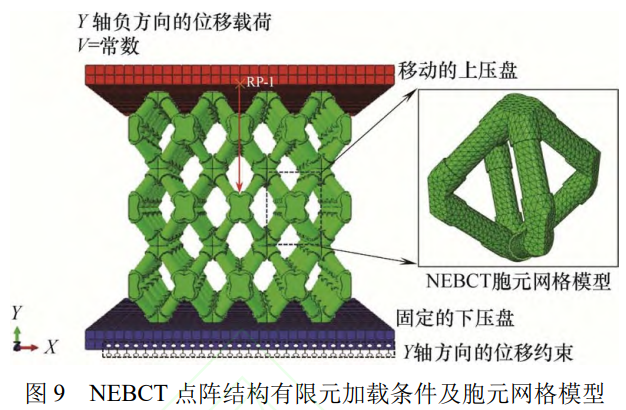
NEBCT 点阵结构准静态压缩仿真加载情况如图 9 所示。与常规型 BCT 点阵相似,在显式动力学下模拟上压盘下压过程,保持应变率为0.001s−1,采用位移边界条件均匀下压 2.54 mm,应变量为整体模型的 20%。
为研究图8中节点区域加强结构长度L1和直径D1对压缩性能的影响,进一步优化节点区域加强结构,本文针对NEBCT点阵结构准静态压缩的有限元模型,在保持相对密度跨度不超过5%的前提下,以L1和D1两个参数为变量共设计9种不同模型。其中加强区域的直径D1和长度L1各3种尺寸,D1分别为0.70
mm、0.75mm、0.80mm,L1分别为0.75mm、0.80mm、0.90mm。不同模型的几何尺寸参数如表4所示。
表 4 节点加强型点阵结构几何尺寸参数
| 模型名称 | 加强区域长度L1/mm | 加强区域直径D1/mm | 相对密度ρ- (%) | 密度ρ/(g/cm³) |
| NEBCT-D70L75 | 0.75 | 0.70 | 16.52% | 0.733 |
| NEBCT-D75L75 | 0.75 | 0.75 | 17.25% | 0.767 |
| NEBCT-D80L75 | 0.75 | 0.80 | 17.96% | 0.793 |
| NEBCT-D70L80 | 0.80 | 0.70 | 16.74% | 0.744 |
| NEBCT-D75L80 | 0.80 | 0.75 | 17.59% | 0.778 |
| NEBCT-D80L80 | 0.80 | 0.80 | 18.42% | 0.815 |
| NEBCT-D70L90 | 0.90 | 0.70 | 17.17% | 0.760 |
| NEBCT-D75L90 | 0.90 | 0.75 | 18.26% | 0.810 |
| NEBCT-D80L90 | 0.90 | 0.80 | 19.35% | 0.859 |
3.3 节点加强区域尺寸对压缩力学性能影响
图 10 展示了三组不同尺寸下的 NEBCT 点阵结构压缩应力应变曲线。从图中可以看出,不同尺寸的 NEBCT 点阵结构都存在明显的弹性阶段、塑性硬化阶段以及断裂阶段。在弹性阶段,当加强区域长度相同时,随着该区域直径的增大,线性曲线的斜率随之增大,与之对应的弹性模量也随之增大。线弹性阶段之后,曲线进入塑性硬化阶段,逐渐展现出缓慢上升趋势直至达到抗压强度。在该阶段随着加强区域直径的增大,抗压强度随之提高,硬化阶段跨度随之缩短,以加强区域长度 0.80 mm 时为例,该区域直径为 0.75 mm 时相较于 0.70 mm 的抗压强度增大了 9.44%,抗压强度对应的应变值下降了 14.99%;当直径为 0.80 mm 时,相较于 0.75 mm 时的抗压强度增大了 4.43%,与之对应的应变下降了 5.27%,可见加强区域直径越低,点阵结构力学性能下降越为明显。
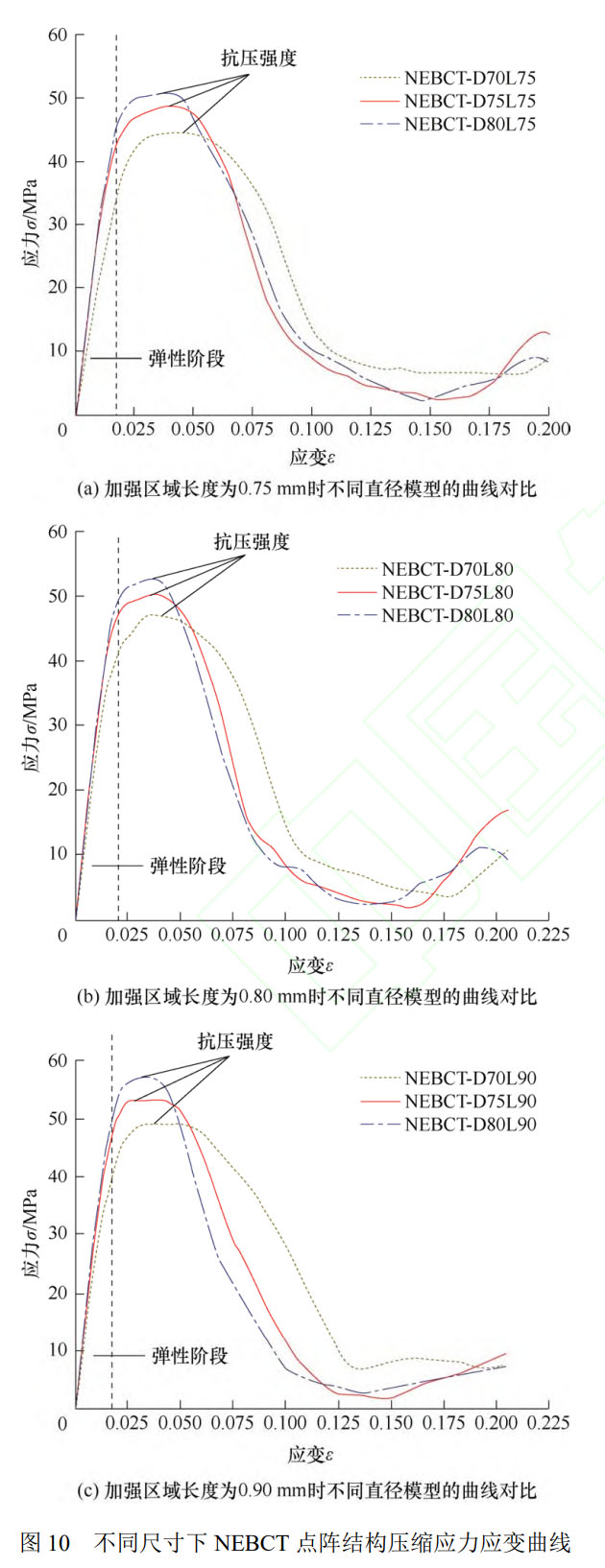
由图 10 可知,节点加强区域的L1和D1参数数值越大,对应的抗压强度越大。但 NEBCT 点阵结构因为增大了节点区域的几何构型,因此其相对密度相较于常规 BCT 点阵结构会有所增加。无论点阵结构的拓扑结构如何,一般来说其力学性能会随着相对密度的提高而提高 [25],所以在进行数据对比时,应引入比弹性模量、比极限强度等以排除相对密度的改变对力学性能的影响,便于比较不同点阵结构之间的性能差异。
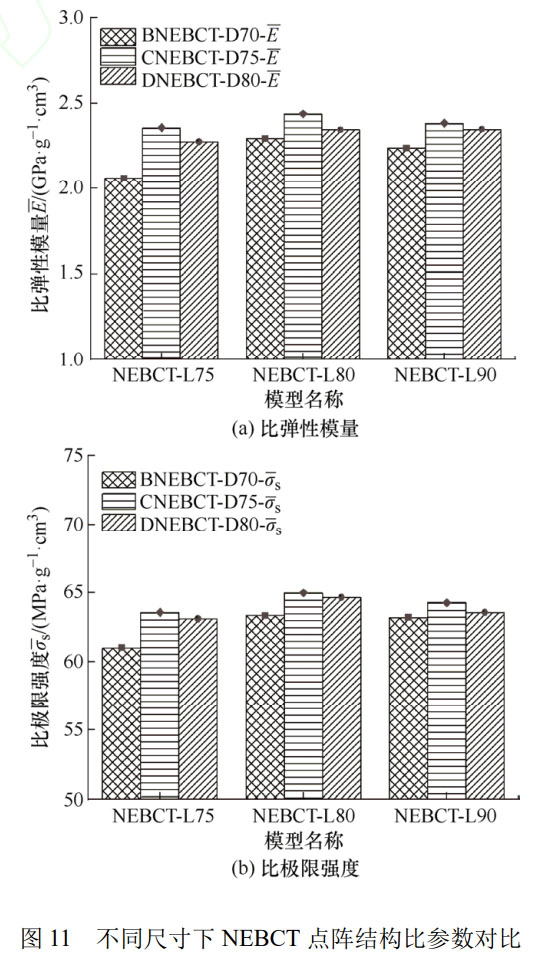
通过图11a的比弹性模量对比发现,不同尺寸下的NEBCT点阵结构比弹性模量差距较大,其中以L1为0.80mm,D1为0.75mm时比弹性模量最大,为2.40GPa.g-1.cm3。当保持加强区域长度不变时,加强区域直径为0.75mm时的比弹性模量最高;当保持加强区域直径不变时,随着该区域长度的变化,比弹性模量呈现出先增大后减小的趋势,可见过高或过低的增强区域直径及长度均会降低点阵结构的力学性能。对于图11b所展示的比极限强度而言,其数值大小受加强区域直径的影响较大,其中以L1为0.80mm,D1为0.75mm时比极限强度最大,为64.99MPa.g-1.
。当加强区域直径为0.70mm和0.80mm时,随着该区域长度的不断增加,比极限强度呈先增加后减小的趋势,且变化幅度较为明显。当加强区域直径为0.75mm时,随着该区域长度的变化,比极限强度基本稳定,虽然存在先增后减的态势,但变化幅度远小于其余直径组。
图 12 对比了不同尺寸下的 NEBCT 点阵结构的能量吸收情况。当应变为 0.02 之前,点阵结构处于弹性变形阶段,能量吸收为 0,当进入塑性硬化阶段时,因为点阵结构出现了永久性塑性变形,所以在这一阶段能量吸收量快速上升,当达到应力峰值后,点阵结构进入断裂阶段,能量吸收曲线进一步上升,直至点阵结构坍塌带闭合后放缓。通过对断裂时刻能量吸收情况分析可得,增强区域的长度和直径越大,能量吸收越大,因为其中包含了相对密度变化的影响,所以通过比能量吸收对比图可知,当增强区域长度为 0.80 mm、直径为 0.75 mm 时的比能量吸收最大,为 4 165.07 mJ/g。
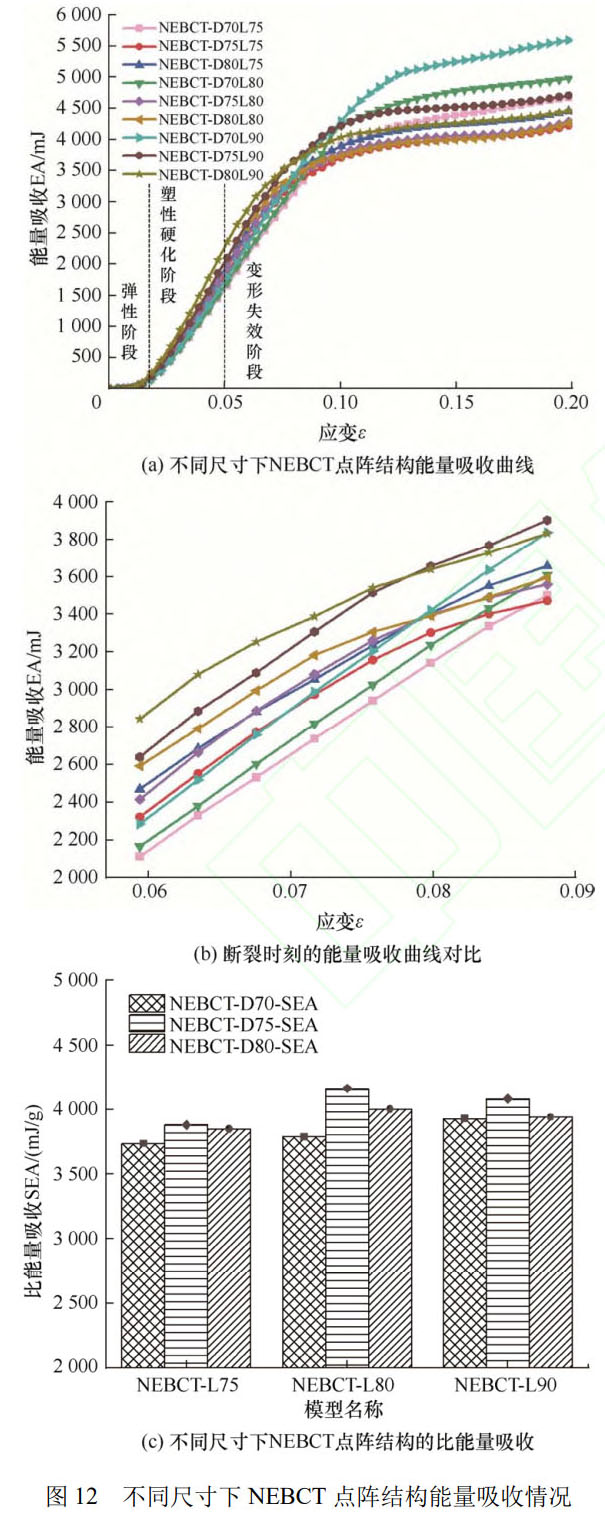
因此,当增强区域长度为 0.8 mm,直径为 0.75 mm 时,NEBCT 点阵结构的力学性能最佳。与常规型 BCT 点阵结构相比,比弹性模量增加了 349.57%,比极限强度提升了 102.26%,表明节点加强区域结构可以显著提升 BCT 点阵结构的力学性能。
3.4 节点加强型点阵结构的失效模式分析
图 13 展示了 NEBCT 点阵结构的压缩变形过程。与常规 BCT 点阵结构相似,在压缩初时刻点阵结构均匀变形,且应力也较为均匀的分布在节点加强区域和与之相连的杆件上。当应变增加到 9.3% 时,节点加强区域出现应力集中现象,抗压强度为 1 258 MPa。应力集中区域分布在与压缩方向垂直的杆件连接带上,并且没有均匀分布在所有节点加强区域,而是仅分布于中间一层点阵胞元。随着应变的进一步增大,NEBCT 点阵结构开始在应力集中区域出现开裂,如图 13c 所示。其整体的变形和失效模式相较于常规 BCT 点阵结构发生了巨大变化,变为横向沉降式坍塌。
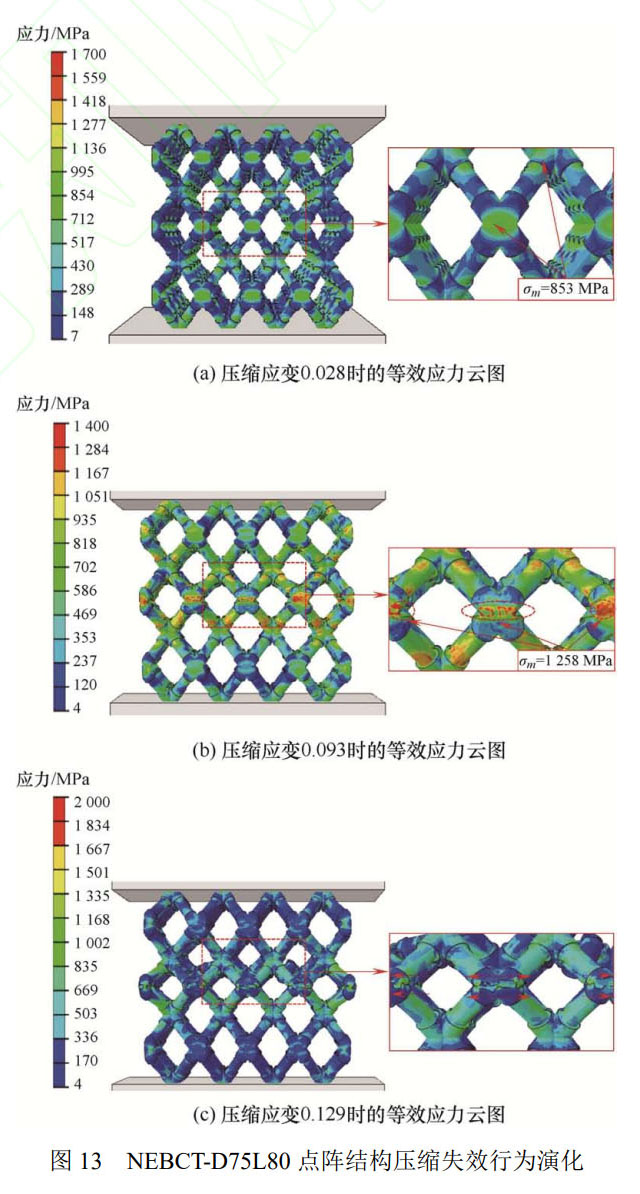
失效模式发生变化的可能原因为,在 NEBCT 点阵结构中,由于节点承载能力的提升,载荷能够更均匀地通过节点传递到连杆上,且点阵结构与上下压盘接触部分由于其进行了增强,使得与上下压盘相接触的杆件不易发生剪切失效,延缓了上下两层胞元整体的塑性变形,于是中间层胞元的最外侧节点区域因为较少的支撑而率先开裂。当外层节点和连杆失效后,载荷会逐渐传递到内层,导致内层节点和连杆开始承受载荷,从而形成横向坍塌的失效模式。进一步结合应力应变曲线分析,NEBCT 点阵结构的压溃变形主要发生在应力应变曲线中的应力下降段,对提高点阵结构抗压强度水平无显著影响。
4、结论
采用有限元仿真方法对常规 BCT 点阵结构进行了准静态压缩模拟,确定了钛合金点阵结构微支柱的力学本构参数并分析了 BCT 点阵结构的失效过程。在此基础上,通过对节点区域进行结构加强,探究加强区域几何参数对点阵结构压缩力学性能的影响规律,主要研究结论如下:
(1) 采用 SLM 制备的常规 BCT 点阵结构因工艺缺陷会导致微支柱力学性能明显下降。为保证仿真结果更具可信度,采用试错法,以应力应变曲线为参照进行微支柱力学本构参数识别。当微支柱力学本构参数中弹性模量为 104 GPa,屈服强度为 811 MPa,强度系数为 214 MPa,硬化指数为 0.45 时,力学性能和变形行为在初期塑性流变区内与实验结果拟合程度较好,可用于节点加强分析。
(2) 常规 BCT 点阵结构失效形式是由节点尤其是外围节点区域应力集中而产生塑性变形,进而扩展到胞元杆件导致外围胞元塌陷,逐渐形成贯穿整体的斜 60° 角的坍塌带。因此节点区域的抗压强度对于点阵结构整体力学性能有较大影响。
(3) 节点加强型点阵结构的失效形式相比于常规 BCT 点阵结构发生改变,由于节点承载能力的提升延缓了上下两层胞元的塑性变形,因此中间层胞元的最外侧节点区域因为较少的支撑而率先开裂,进而引发横向沉降式坍塌。
(4) 对比不同尺寸下的节点加强型点阵结构的仿真结果,比参数呈现出先增大后减小的趋势。加强区域长度为 0.8 mm,直径为 0.75 mm 的节点加强型点阵结构力学性能最佳,其比能量吸收为 4 165.07 mJ/g,比弹性模量相较于常规 BCT 点阵结构增加了 349.57%,比极限强度提升了 102.26%。因此在 BCT 点阵结构节点处引入 X 型加强区域可以显著提升点阵结构力学性能。
参 考 文 献
[1] KHAN N,RICCIO A. A systematic review of design for additive manufacturing of aerospace lattice structures: Current trends and future directions [J]. Progress in Aerospace Sciences,2024,149:101021.
[2] MACONACHIE T,LEARY M,LOZANOVSKI B,et al. SLM lattice structures :Properties ,performance , applications and challenges [J]. Materials & Design,2019, 183:108137.
[3] CHANG Chao,WU Wei,ZHANG Hui,et al. Mechanical characteristics of superimposed 316L lattice structures under static and dynamic loading [J]. Advanced Engineering Materials,2021,23 (7):2001536.
[4] 张阳,张同庆,刘磊,等。基于 BCC 点阵填充的控制臂结构优化 [J]. 机械设计,2024,41 (6):40-46. ZHANG Yang,ZHANG Tongqing,LIU Lei,et al. Structure optimization of control arm based on BCC lattice filling [J]. Journal of Machine Design,2024,41 (6): 40-46.[5] ELAMBASSERIL J,LU S L,NING Y P,et al. 3D characterization of defects in deep-powder-bed manufactured Ti-6Al-4V and their influence on tensile properties [J]. Materials Science and Engineering:A, 2019,761:138031.
[6] 司冠琛,向政,杨琴,等。单胞构型和微观缺陷对 SLM 制备 NiTi 合金高刚度点阵结构疲劳性能的影响 [J]. 激光与光电子学进展,2023,60 (21):230-240. SI Guanchen,XIANG Zheng,YANG Qin,et al. Effects of cell configuration and micro defects on fatigue properties of NiTi alloy lattice structure having with rigidity prepared by SLM [J]. Laser & Optoelectronics Progress,2023,60 (21):230-240.
[7] 李九霄,李鸣佩,杨东野,等。选择性激光熔化制造金属构件残余应力的研究进展 [J]. 机械工程材料,2018, 42 (8):1-6. LI Jiuxiao,LI Mingpei,YANG Dongye,et al. Research progress on residual stress in metal component manufactured by selective laser melting [J]. Materials for Mechanical Engineering,2018,42 (8):1-6.
[8] BAI Long. Multi-objective structural optimization design of Ti6Al4V lattice structure formed by SLM [J]. Journal of Mechanical Engineering,2018,54 (5):156.
[9] 熊飞. SLM 制备的 Ti6Al4V 轻质点阵结构多目标结构优化设计研究 [D]. 重庆:重庆大学,2017. XIONG Fei. Multi-objective structural optimization design of Ti6Al4V lattice Structure by SLM [D]. Chongqing:Chongqing University,2017.
[10] WU Bin ,SUN Feifan ,WANG Lizhe ,et al. Characterization of mechanical equivalent properties for node enhanced graded lattice structure [J]. Modelling and Simulation in Materials Science and Engineering,2023, 31 (6):065016.
[11] XU Hanwen ,LIU Changmeng ,MAO Hao,et al. Strengthening nodes to obtain high-strength pyramid lattice structure by using wire arc additive manufacturing method [J]. Journal of Manufacturing Processes,2024, 117:125-133.
[12] 姚定烨,兰彦宇,马宇立,等。基于选区激光熔化的 Ti-6Al-4V 钛合金节点增强型点阵结构及其力学行为 [J]. 热加工工艺,2023,52 (13):121-126. YAO Dingye,LAN Yanyu,MA Yuli,et al. Ti-6Al-4V node-enhanced lattice structure prepared by selective laser melting and its mechanical behavior [J]. Hot Working Technology,2023,52 (13):121-126.
[13] 孙思远,盛亚鹏,段玥晨,等。拓扑优化体心立方结构平压性能研究 [J]. 复合材料科学与工程,2025 (3):7-14. SUN Siyuan,SHENG Yapeng,DUAN Yuechen,et al. Flatwise compression property of topology optimized body centered cubic structures [J]. Composites Science and Engineering,2025 (3):7-14.
[14] ZHAO Miao,ZHANG D Z,LI Zhonghua,et al. Design, mechanical properties,and optimization of BCC lattice structures with taper struts [J]. Composite Structures, 2022,295:115830.
[15] MEYER G,WANG Haixu,MITTELSTEDT C. Influence of geometrical notches and form optimization on the mechanical properties of additively manufactured lattice structures [J]. Materials & Design,2022,222:111082.
[16] TAN Zhen,JIANG Xinyi,XI Zhao,et al. Fabrication of Zr-based bulk metallic glass lattice structure with high specific strength by laser powder bed fusion [J]. Additive Manufacturing,2024,95:104556.
[17] ROACH A M,WHITE B C,GARLAND A,et al. Size-dependent stochastic tensile properties in additively manufactured 316L stainless steel [J]. Additive Manufacturing,2020,32:101090.
[18] 蒋华臻,房佳汇钰,陈启生,等。激光选区熔化成形 316L 不锈钢工艺、微观组织、力学性能的研究现状 [J]. 中国激光,2022,49 (14):1402804. JIANG Huazhen,FANG Jiahuiyu,CHEN Qisheng,et al. State of the art of selective laser melted 316L stainless steel :Process ,microstructure ,and mechanical properties [J]. Chinese Journal of Lasers,2022,49 (14): 1402804.
[19] CAO Xiaofei,JIANG Yongbo,ZHAO Tian,et al. Compression experiment and numerical evaluation on mechanical responses of the lattice structures with stochastic geometric defects originated from additive-manufacturing [J]. Composites Part B : Engineering,2020,194:108030.
[20] LI Peiyao,SUN Wenbo,ZHANG Weihong,et al. Effect of geometric defects on the mechanical properties of additive manufactured Ti6Al4V lattice structures [J]. Thin-Walled Structures,2024,205:112497.
[21] HOSSAIN U,GHOUSE S,NAI K,et al. Mechanical and morphological properties of additively manufactured SS316L and Ti6Al4V micro-struts as a function of build angle [J]. Additive Manufacturing,2021,46:102050.
[22] ARAGHI M,ROKHGIREH H,NAYEBI A. Experimental and FEM investigation of BCC lattice structure under compression test by using continuum damage mechanics with micro-defect closure effect [J]. Materials & Design, 2023,232:112125.
[23] HASAN R ,MINES R A W ,TSOPANOS S. Determination of elastic modulus value for selectively laser melted titanium alloy [J]. Journal of Mechanical Engineering and Technology,2010,2:17-26.
[24] WANG Zhiyong ,LI Peifeng. Characterisation and constitutive model of tensile properties of selective laser melted Ti-6Al-4V struts for microlattice structures [J]. Materials Science and Engineering:A,2018,725: 350-358.
[25] BURTON H E,EISENSTEIN N M,LAWLESS B M, et al. The design of additively manufactured lattices to increase the functionality of medical implants [J]. Materials Science & Engineering C ,Materials for Biological Applications,2019,94:901-908.
作者简介
李国举,男,1986 年出生,博士,副教授,硕士研究生导师。主要研究方向为点阵结构材料轻量化设计。E-mail:liguoju@zua.edu.cn
张昕喆 (通信作者),男,1988 年出生,博士,副教授,硕士研究生导师。主要研究方向为飞行器结构设计。E-mail:zxzzua@zua.edu.cn
(注,原文标题:钛合金体心四方点阵结构压缩性能优化分析)
相关链接